Magnitude and Direction

Each vector holds the magnitude as well as the direction of the movement.

Lets calculate both for vector \vec{x}=\begin{bmatrix} 4\\2\end{bmatrix}.

The symbol we use for the magnitude is \left | \right |.

To calculate the magnitude of a 2D vector we will use the Pythagorean Theorem.

In our example the magnitude will be calculated the following way:

\left |\vec{x} \right |=\sqrt{4^2+2^2}

Where 4 is the horizontal component of the vector and 2 is the vertical.

To calculate the direction of the movement we will use an angle. We can use Degrees or Radians. In this example we will focus on Degree. (It is always possible to move Degrees to Radians and vice versa).

lets look at the vector \vec{x} again. It has an angle \theta with respect to the horizontal axis.

Please take a look at the picture below for an illustration:

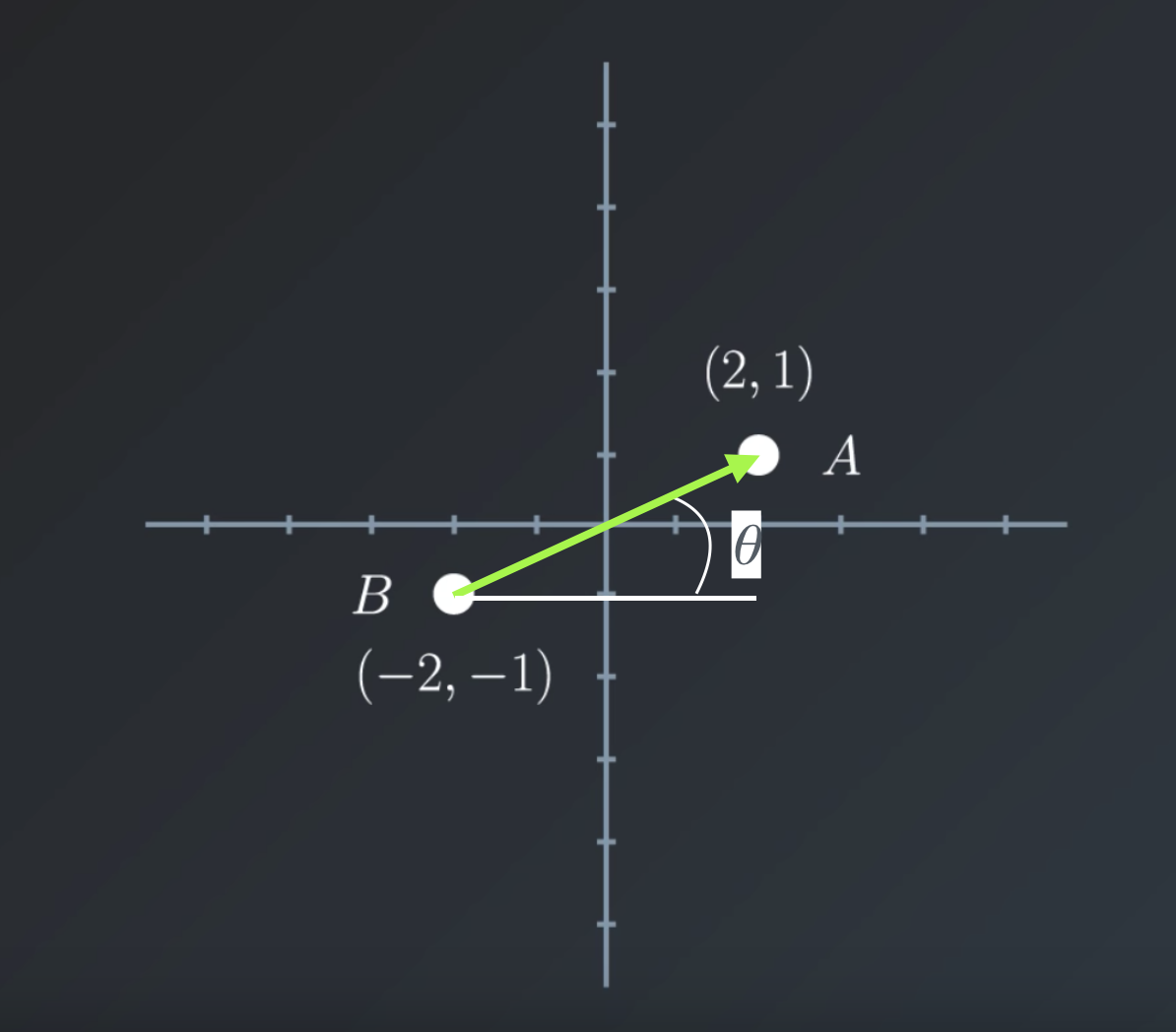
To calculate \theta we will use what we remember from Trigonometry!

In the specific angle illustrated below \theta is calculated the following way:

\theta=tan^{-1}\frac{y}{x}

Equation 3

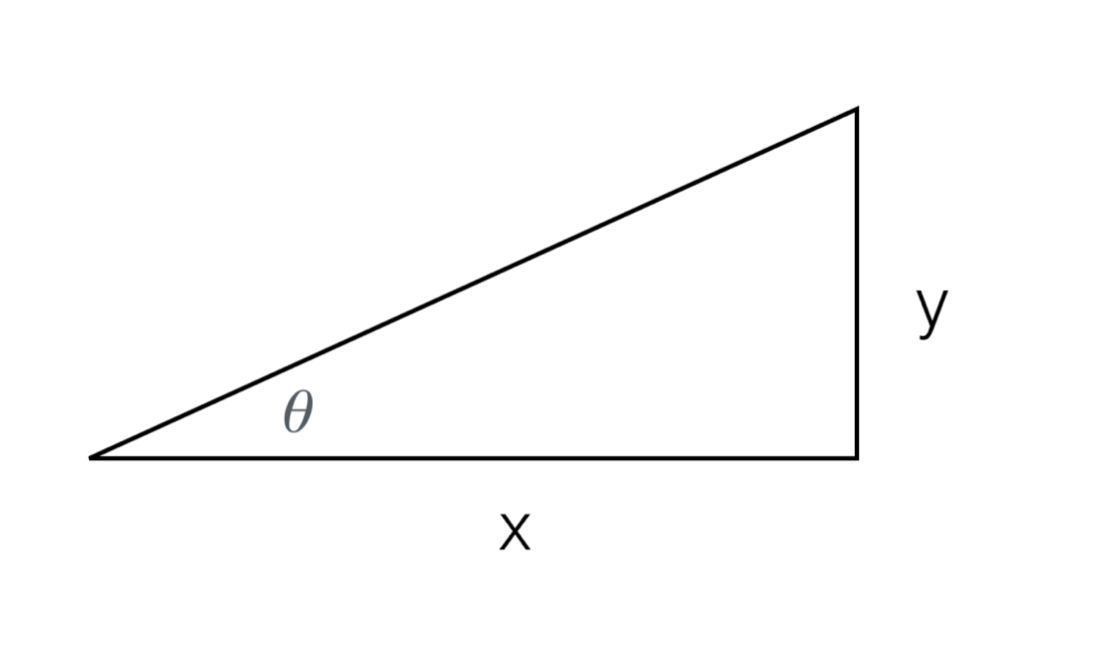
Therefore, in our case

\theta=tan^{-1}\frac{2}{4}=26.56505^{\circ}

For further information on magnitude and direction of a 2D vector, please use the following link